Hello,
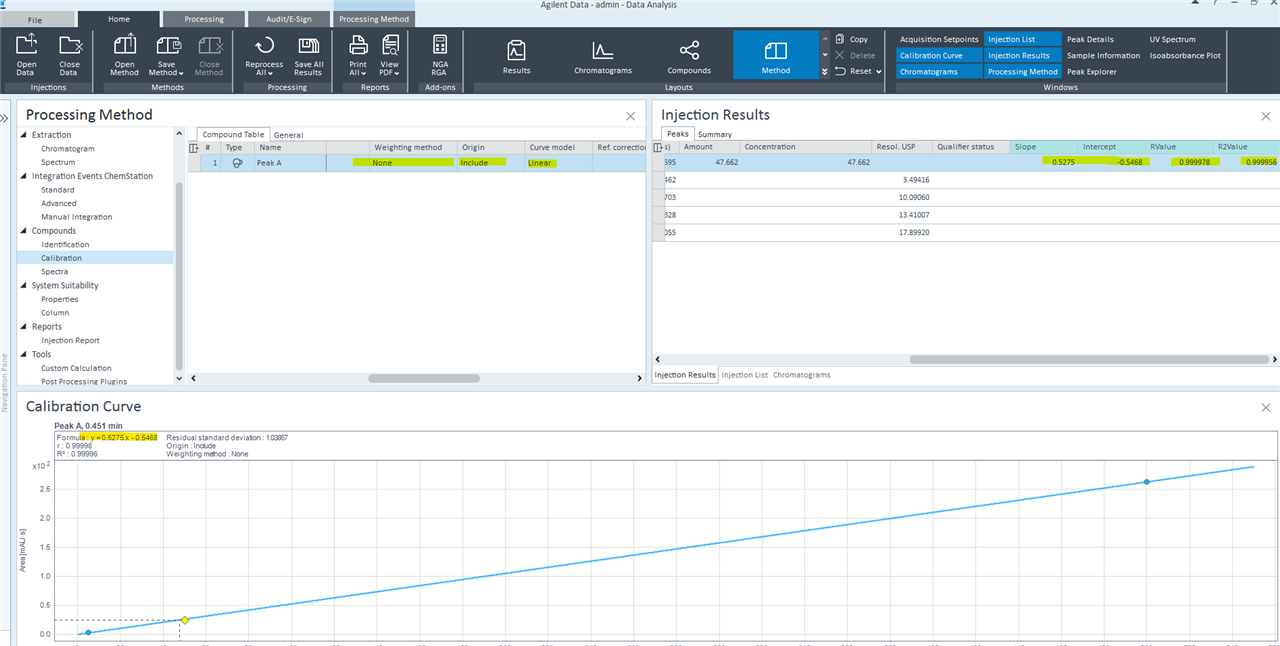
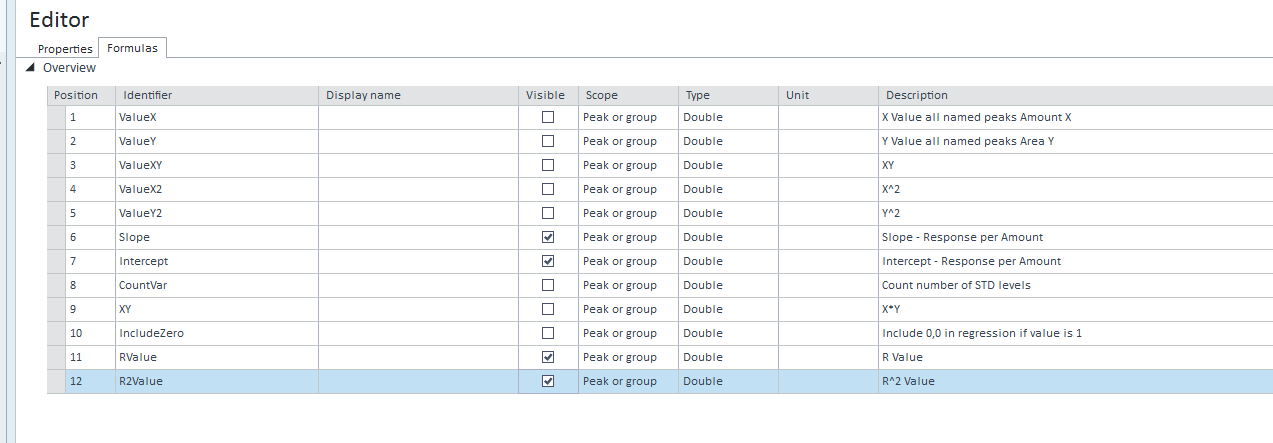
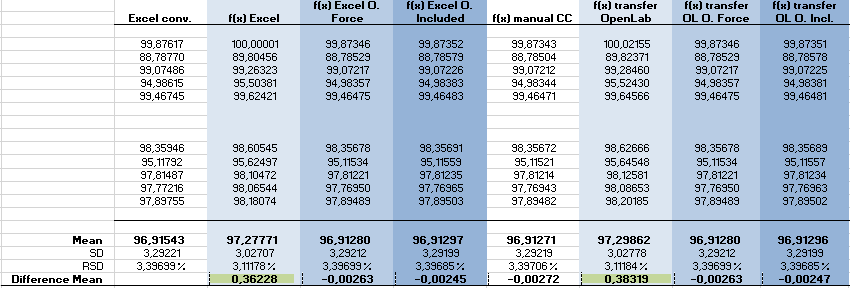
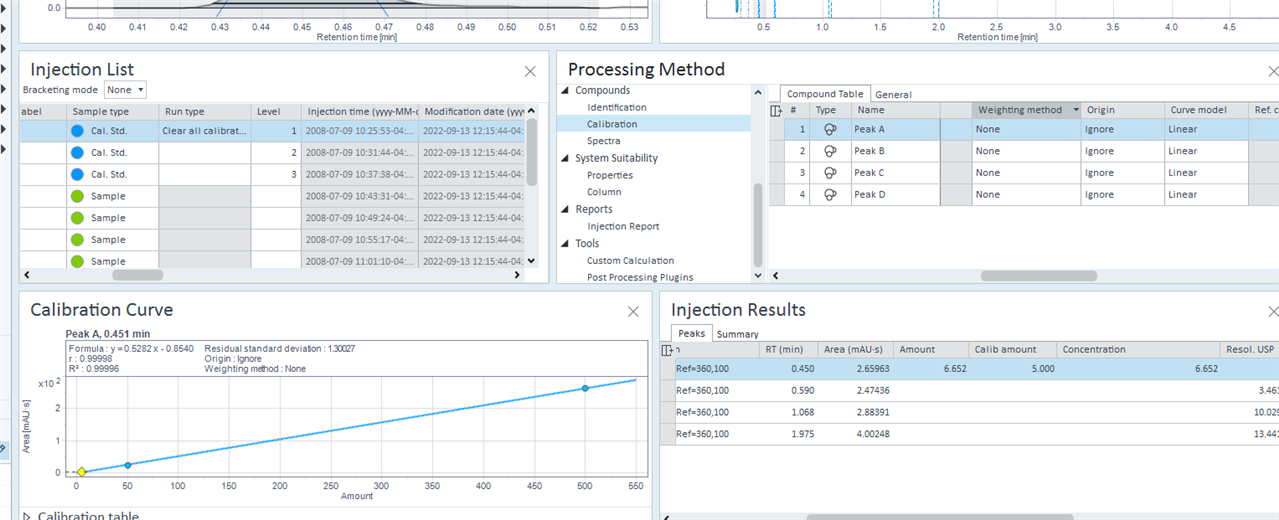
Is there a possibility in OpenLab 2.5 to add level specific dilution factors in the compound table of the calibration? Is there possibly an approach via a Custom Calculation?
In detail, it is a multi point calibration with three calibration levels. For each substance, there are three stock solutions with weights of the same quantity per level.
For the preparation of the following working standards, substance-specific dilution factors are specified, resulting in three multi-substance solutions in the concentrations 50%, 75% and 100%.
In addition, we use the bracketing mode of the Injection List, which could make our project even more complicated.

Thank you and best regards,
coh